A Weighty Matter
Removing Weights From a Barbell
One of the hobbies that I have taken up over the past few years has been lifting weights. I mostly follow powerlifting style routines, and those tend to involve relatively long rests between sets which leaves a lot of idle time. During one such break recently, I began to ponder the different orders one could remove the weights from a barbell.
One mistake people have to make at least once is to absentmindedly remove all of the weights from one side of the bar. This works up to a point, but if there is enough weight on the other side, the bar will dramatically tip over and the weights will come crashing down. As a practical matter, you can get away with a difference of two 45 lb plates between the sides, though a difference of three plates spells disaster. The general advice to avoid this is to simply remove the weights from alternating sides, keeping the center of gravity between the supports. To be impractical, given that you start with n plates on each side, how many ways can you remove them, both safely and unsafely?
Unconstrained Problem
Let’s tackle the simpler problem first, where we ignore physics and don’t restrict how unbalanced the bar can be. Given n weights on each side, let ![]() be the total number of ways to remove them. Label weights on each side
be the total number of ways to remove them. Label weights on each side ![]() , and
, and ![]() , going from the outside in. Below is an example for
, going from the outside in. Below is an example for ![]() :
:
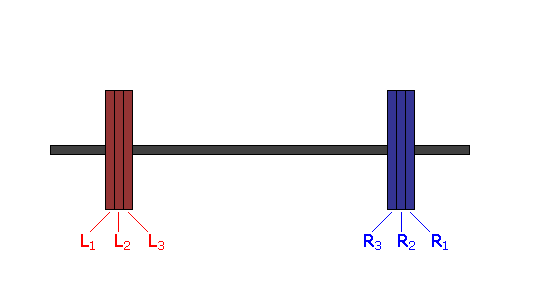
For this case, we can simply list all twenty possible removal orders by inspection:
- L1, L2, L3, R1, R2, R3
- L1, L2, R1, L3, R2, R3
- L1, L2, R1, R2, L3, R3
- L1, L2, R1, R2, R3, L3
- L1, R1, L2, L3, R2, R3
- L1, R1, L2, R2, L3, R3
- L1, R1, L2, R2, R3, L3
- L1, R1, R2, L2, L3, R3
- L1, R1, R2, L2, R3, L3
- L1, R1, R2, R3, L2, L3
- R1, L1, L2, L3, R2, R3
- R1, L1, L2, R2, L3, R3
- R1, L1, L2, R2, R3, L3
- R1, L1, R2, L2, L3, R3
- R1, L1, R2, L2, R3, L3
- R1, L1, R2, R3, L2, L3
- R1, R2, L1, L2, L3, R3
- R1, R2, L1, L2, R3, L3
- R1, R2, L1, R3, L2, L3
- R1, R2, R3, L1, L2, L3
If we were to list all the permutations of the six plates, there would be 6! = 720 possible combinations. But, notice that even though the left right order changes, we always take off the plates from the outside first, so L1 always precedes L2 which always precedes L3. For each of the listed orders, you could permute the three left plates in 3!=6 ways, and the three right plates in six ways. Thus, each of the listed orders corresponds to 36 of the 720 total combinations. Generalizing this observation, there are a total of
(1) ![]()
possible unconstrained orders. Given 2n slots, we essentially choose where to place the n left (red) plates. That was easy!
Constrained Problem
Things get more complicated when we restrict how unbalanced the loading can be. At any point in time, define a signed delta loading by the number of plates still on the bar:
(2) ![]()
We always start out with ![]() , and we end up there as well. For a particular removal order, let
, and we end up there as well. For a particular removal order, let ![]() be the maximum value that
be the maximum value that ![]() reaches at some point during the process, and let
reaches at some point during the process, and let ![]() be the number of ways to remove n plates that have
be the number of ways to remove n plates that have ![]() exactly equal to m. It’s clear the minimum and maximum of
exactly equal to m. It’s clear the minimum and maximum of ![]() are 1 and n respectively, and these are the easiest cases to count directly.
are 1 and n respectively, and these are the easiest cases to count directly.
If we limit ![]() to 1 (the physically safe option, and what you should do in practice), we can think of each pair of plates as joined, and we simply choose one of two orders, LR or RL, for each independently. Thus, there are a total of
to 1 (the physically safe option, and what you should do in practice), we can think of each pair of plates as joined, and we simply choose one of two orders, LR or RL, for each independently. Thus, there are a total of ![]() removal orders with a
removal orders with a ![]() :
:
(3) ![]()
The number of removal orders with ![]() is even simpler. To reach that
is even simpler. To reach that ![]() , you have to remove all of the plates on one side before removing any from the other, so it’s literally just a choice between two orders: LL…LRR…R and RR…RLL…L
, you have to remove all of the plates on one side before removing any from the other, so it’s literally just a choice between two orders: LL…LRR…R and RR…RLL…L
(4) ![]()
For our example problem with three plates, that means ![]() and
and ![]() , from which we can deduce that
, from which we can deduce that ![]() . That works for this small case, but how can we calculate these medial values directly? To answer this, let’s introduce a way to visualize removal orders.
. That works for this small case, but how can we calculate these medial values directly? To answer this, let’s introduce a way to visualize removal orders.
Removal Order Graph
The graph below shows a potential order to remove weights with n=4. We start in the upper left corner with four weights on each side. If we remove a weight from the right side of the bar, we travel right on the graph, and if we remove a weight from the left side, we travel down. The path always starts on the upper left corner and always terminates at the lower right corner. Since we don’t add plates back to the bar, we can never travel left or up on the graph.
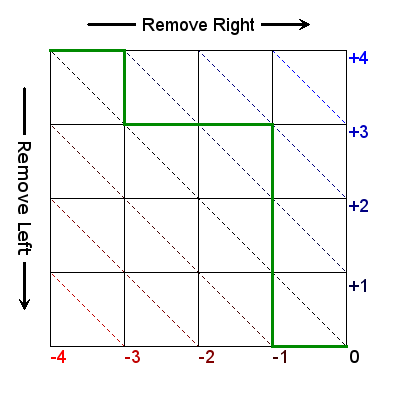
Particular values of ![]() correspond to the labeled diagonals. For the case of the example path shown in green,
correspond to the labeled diagonals. For the case of the example path shown in green, ![]() reaches a high of 2 before doing down to a low of -1, thus making
reaches a high of 2 before doing down to a low of -1, thus making ![]() for this path.
for this path.
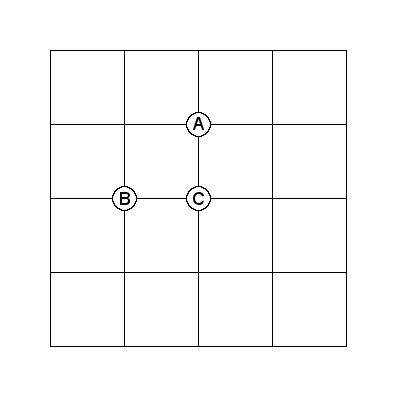
Since paths on this graph travel in only two directions, to arrive at node C, you would have to first path through either node A or node B. This means that if we know the number of paths that go through both nodes, ![]() and
and ![]() , then we can simply sum them to get the number of paths that go through node C:
, then we can simply sum them to get the number of paths that go through node C:
(5) ![]()
We can easily do this for all the nodes in the graph, with the initial condition that there is one way to get to the starting node. For the unconstrained case we have:
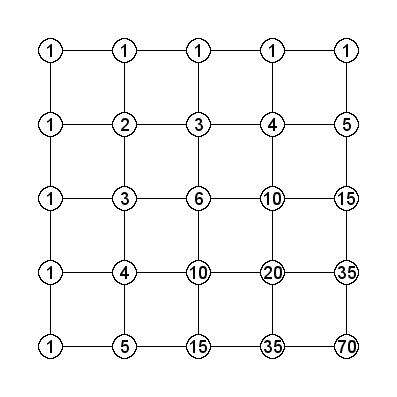
Since we can’t travel up, the nodes along the top of the graph inherit the number paths from the node to the left. This corresponds to just taking all the plates from the right side one by one. Similarly for the left side. So, by summing the nodes on the graph, we conclude there are 70 ways to remove four plates. This matches our earlier calculation from eq. 1. Observant readers will notice this is just a truncation of Pascal’s triangle. Individual nodes in the triangle can be calculated directly via binomial coefficients, due to the identity:
(6) ![]()
Which can be seen as another way of arriving at eq. 1.
Instead of directly calculating ![]() , we can instead calculate all the paths with
, we can instead calculate all the paths with ![]() less than or equal to three. Denote this by:
less than or equal to three. Denote this by:
(7) 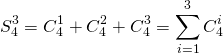
We can represent this on our graph by simply setting unreachable nodes to zero, i.e. setting the upper right and lower left nodes to zero:
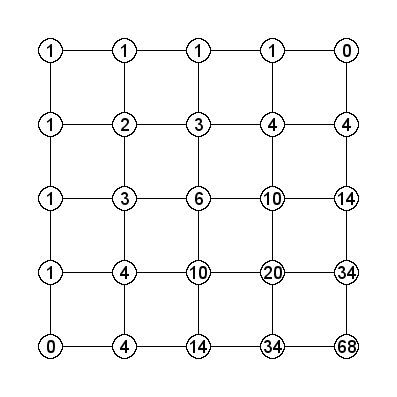
Which means there are a total of 68 ways to remove four plates without letting ![]() exceed three. Similarly, limiting it to a two plate difference gives:
exceed three. Similarly, limiting it to a two plate difference gives:
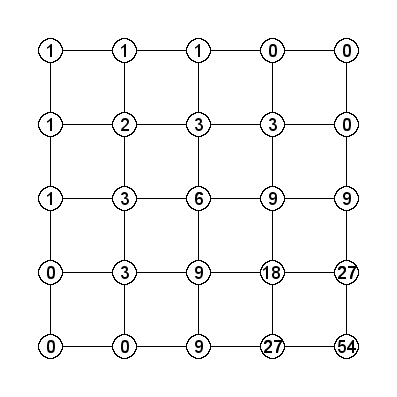
And hence, ![]() , and we can conclude that:
, and we can conclude that:
(8) ![]()
And finally, when we limit the differential to one plate:
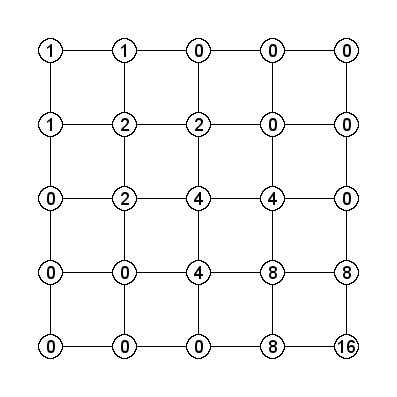
Which validates the result from eq. 3.
Recursive Solution
The unconstrained problem had a compact answer in eq. 1, but I can’t see any concise way to describe the solution described above using binomial coefficients. However, we can describe the answer recursively. Label the nodes following the order of binomial coefficients in Pascal’s triangle:
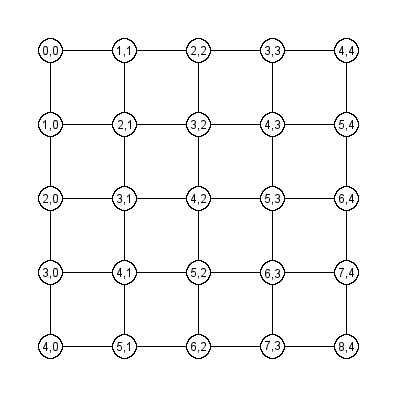
Let ![]() be the value of node
be the value of node ![]() with the constraint that
with the constraint that ![]() . We can calculate
. We can calculate ![]() directly for each node:
directly for each node:
(9) ![]()
And thus we can recursively calculate:
(10) 
And now we have a method to solve our very pressing problem!